Khoảng Cách Giữa Hai Đường Thẳng Chéo Nhau: Hướng Dẫn Chi Tiết và Phương Pháp Giải

Giới Thiệu Tổng Quan

Khái Niệm Cơ Bản

Khoảng cách giữa hai đường thẳng chéo nhau là độ dài của đoạn thẳng ngắn nhất nối hai đường thẳng đó. Đây là một khái niệm quan trọng trong hình học không gian và có nhiều ứng dụng thực tiễn trong kiến trúc, xây dựng và thiết kế 3D.

Tầm Quan Trọng

• Ứng dụng trong thiết kế công trình
• Giải quyết bài toán về kết cấu
• Tính toán trong không gian ba chiều
• Ứng dụng trong đồ họa máy tính

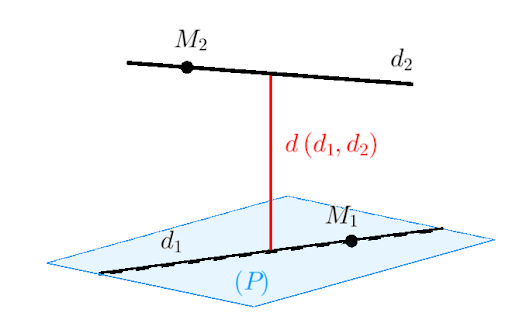
Các Đặc Điểm Của Đường Thẳng Chéo Nhau

Định Nghĩa

Hai đường thẳng được gọi là chéo nhau khi chúng:

1. Không cắt nhau
2. Không song song với nhau
3. Không nằm trong cùng một mặt phẳng

Tính Chất Đặc Biệt

• Luôn tồn tại một và chỉ một đường thẳng vuông góc chung
• Khoảng cách giữa chúng là độ dài của đường vuông góc chung
• Đường vuông góc chung là đoạn ngắn nhất nối hai đường thẳng

Phương Pháp Tính Khoảng Cách

Công Thức Tổng Quát

Nếu hai đường thẳng d₁ và d₂ có phương trình vector:

d₁: r₁ = a₁ + λv₁
d₂: r₂ = a₂ + μv₂

Thì khoảng cách d giữa chúng được tính bởi công thức:

d = |[(a₂ - a₁).(v₁ × v₂)]| / |v₁ × v₂|

Các Bước Giải Chi Tiết

1. Xác định vector chỉ phương của hai đường thẳng
2. Tìm một điểm thuộc mỗi đường thẳng
3. Áp dụng công thức tính khoảng cách
4. Kiểm tra kết quả

Ví Dụ Minh Họa

Bài Toán Mẫu

Cho hai đường thẳng:

d₁: (x-1)/2 = (y+1)/3 = (z-2)/4
d₂: x = 2t+1, y = 3t-2, z = t+5

Tính khoảng cách giữa hai đường thẳng này.

Phương Pháp Giải

1. Vector chỉ phương của d₁: v₁(2,3,4)
2. Vector chỉ phương của d₂: v₂(2,3,1)
3. Điểm A₁(1,-1,2) thuộc d₁
4. Điểm A₂(1,-2,5) thuộc d₂
5. Áp dụng công thức tính khoảng cách

Các Dạng Bài Tập Thường Gặp

Dạng 1: Hai Đường Thẳng Cho Bởi Phương Trình Tham Số

• Phương pháp chuyển về dạng vector
• Cách xác định điểm thuộc đường thẳng
• Tính toán khoảng cách

Dạng 2: Hai Đường Thẳng Cho Bởi Phương Trình Canonical

• Chuyển về phương trình tham số
• Xác định vector chỉ phương
• Áp dụng công thức tính khoảng cách

Phương Pháp Học Hiệu Quả

Chiến Lược Học Tập

1. Nắm vững lý thuyết cơ bản
2. Luyện tập nhiều dạng bài tập
3. Học theo phương pháp tư duy logic
4. Áp dụng công nghệ hỗ trợ học tập

Tài Nguyên Học Tập

Để học tốt chủ đề này, bạn có thể tham khảo các khóa học trực tuyến tại Toliha:

• Khóa học Hình học không gian nâng cao
• Video bài giảng chuyên đề
• Bài tập có lời giải chi tiết
• Tài liệu tham khảo chuyên sâu

Lời Khuyên và Mẹo Học Tập

Cách Tiếp Cận Bài Toán

1. Đọc kỹ đề bài và xác định dữ kiện
2. Vẽ hình minh họa
3. Lập phương trình và áp dụng công thức
4. Kiểm tra tính hợp lý của kết quả

Tránh Sai Lầm Phổ Biến

• Nhầm lẫn vector chỉ phương
• Sai sót trong tính toán đại số
• Không kiểm tra điều kiện bài toán
• Quên chuyển đổi đơn vị đo

Thông Tin Hỗ Trợ Học Tập

Để được hỗ trợ thêm về chủ đề này và các nội dung học tập khác, bạn có thể liên hệ với Học trực Tuyến Toliha qua:

• Hotline: 0901 86 8899
• Email: [email protected]
• Website: https://toliha.vn

Đội ngũ giáo viên giàu kinh nghiệm tại Toliha luôn sẵn sàng giải đáp mọi thắc mắc và hỗ trợ bạn trong quá trình học tập. Truy cập website https://toliha.vn để tham gia các khóa học trực tuyến chất lượng cao và tài liệu học tập hữu ích.

Kết Luận

Khoảng cách giữa hai đường thẳng chéo nhau là một chủ đề quan trọng trong hình học không gian. Việc nắm vững kiến thức này không chỉ giúp bạn giải quyết tốt các bài tập trong chương trình học mà còn có nhiều ứng dụng thực tiễn. Hãy tận dụng các tài nguyên học tập tại Toliha để phát triển kỹ năng và kiến thức của bạn trong lĩnh vực này.