Hệ Thức Lượng Trong Tam Giác Thường: Khám Phá Chi Tiết

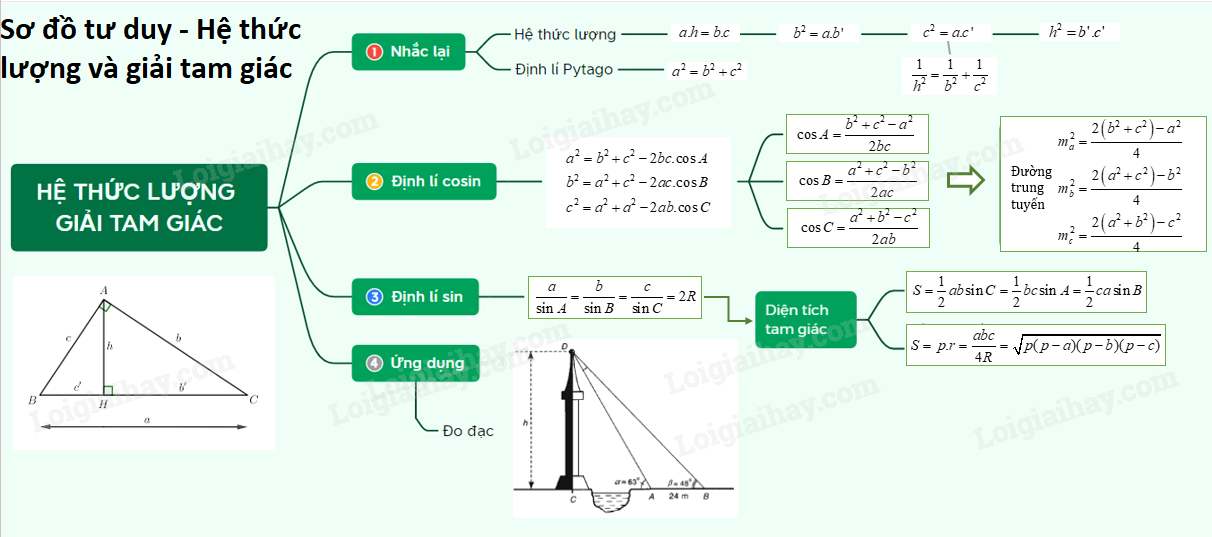
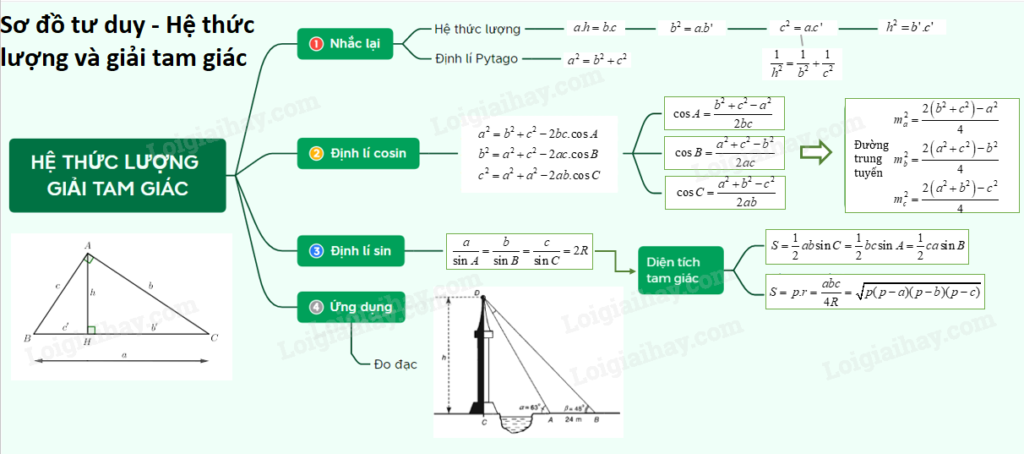
Hệ thức lượng trong tam giác là một trong những chủ đề quan trọng trong toán học, đặc biệt là trong hình học. Những công thức này không chỉ giúp chúng ta giải quyết các bài toán liên quan đến tam giác mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực khác nhau. Trong bài viết này, chúng ta sẽ khám phá chi tiết về các hệ thức lượng trong tam giác thường, cách áp dụng chúng, và các ví dụ minh họa cụ thể. Đồng thời, chúng tôi cũng sẽ giới thiệu trang web toliha.vn, một nguồn tài liệu hữu ích cho việc học tập và ôn luyện toán học trực tuyến.

1. Giới Thiệu Chung Về Hệ Thức Lượng Trong Tam Giác

Hệ thức lượng trong tam giác là những công thức toán học cho phép chúng ta tính toán các đại lượng như độ dài cạnh, góc, và diện tích của tam giác khi biết một số yếu tố nhất định. Các hệ thức này bao gồm định lý Sin, định lý Cosin, và các công thức về đường trung tuyến, độ dài cạnh, và diện tích tam giác.

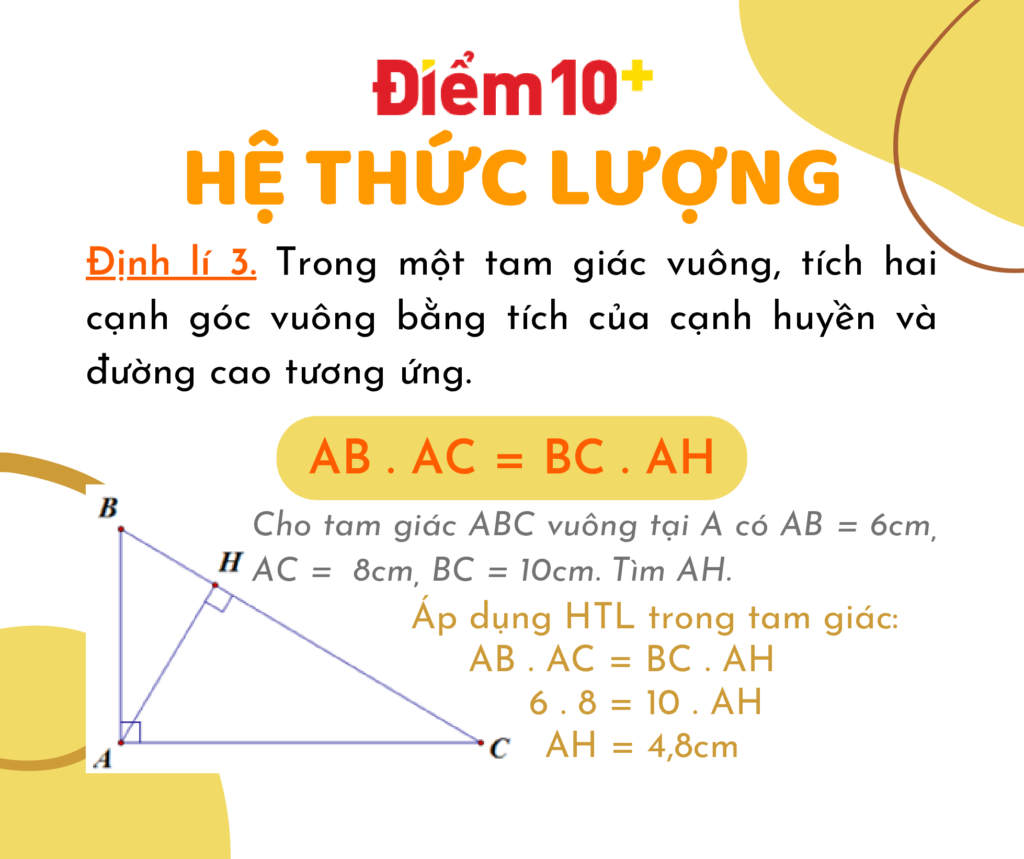
2. Định Lý Sin

Định lý Sin là một trong những hệ thức lượng cơ bản nhất trong tam giác. Định lý này phát biểu rằng trong một tam giác bất kỳ, tỉ số giữa độ dài một cạnh và sin của góc đối diện bằng đường kính của đường tròn ngoại tiếp tam giác đó. Công thức của định lý Sin như sau:

sinAa​=sinBb​=sinCc​=2R

Trong đó:

• a, b, c: Độ dài các cạnh của tam giác.
• A, B, C: Các góc đối diện với các cạnh tương ứng.
• R: Bán kính của đường tròn ngoại tiếp tam giác².

3. Định Lý Cosin

Định lý Cosin cho phép chúng ta tính độ dài cạnh thứ ba của tam giác khi biết hai cạnh và góc xen giữa. Công thức của định lý Cosin như sau:

c2=a2+b2−2abcosC

Trong đó:

• a, b, c: Độ dài các cạnh của tam giác.
• C: Góc xen giữa hai cạnh a và b³.

4. Đường Trung Tuyến

Đường trung tuyến của tam giác là đoạn thẳng nối từ một đỉnh đến trung điểm của cạnh đối diện. Độ dài của đường trung tuyến từ một đỉnh đến cạnh đối diện được tính bằng công thức:

ma2​=42(b2+c2)−a2​

Trong đó:

• m_a: Độ dài đường trung tuyến từ đỉnh A đến cạnh BC.
• a, b, c: Độ dài các cạnh của tam giác.

5. Diện Tích Tam Giác

Diện tích của tam giác có thể được tính bằng nhiều cách khác nhau, bao gồm sử dụng đường cao và cạnh đáy, áp dụng định lý Heron, và sử dụng bán kính của đường tròn ngoại tiếp. Một số công thức tính diện tích tam giác bao gồm:

• Sử dụng đường cao và cạnh đáy:S=21​absinC
• Áp dụng định lý Heron:S=p(p−a)(p−b)(p−c)​Trong đó, (p) là nửa chu vi của tam giác:p=2a+b+c​
• Sử dụng bán kính của đường tròn ngoại tiếp:S=4Rabc​

Trong đó:

• a, b, c: Độ dài các cạnh của tam giác.
• R: Bán kính của đường tròn ngoại tiếp tam giác.

6. Các Ứng Dụng Thực Tiễn Của Hệ Thức Lượng Trong Tam Giác

Hệ thức lượng trong tam giác không chỉ là những công thức toán học mà còn có nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày và các lĩnh vực khoa học kỹ thuật:

• Kiến Trúc và Xây Dựng: Trong kiến trúc và xây dựng, các hệ thức lượng trong tam giác được sử dụng để tính toán các kích thước và góc của các cấu trúc, đảm bảo tính chính xác và an toàn.
• Trắc Địa: Trong trắc địa, các hệ thức lượng trong tam giác được sử dụng để đo đạc và tính toán khoảng cách, diện tích của các khu vực địa lý.
• Thiết Kế Đồ Họa: Trong thiết kế đồ họa, các hệ thức lượng trong tam giác được sử dụng để tạo ra các hình dạng và cấu trúc phức tạp, đảm bảo tính thẩm mỹ và chính xác.

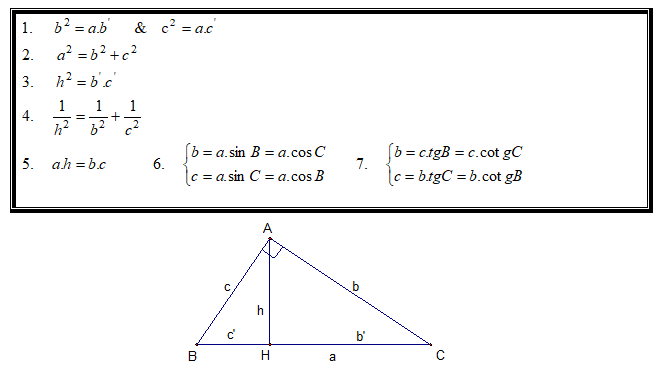
7. Ví Dụ Minh Họa

Để hiểu rõ hơn về cách áp dụng các hệ thức lượng trong tam giác, hãy xem xét một số ví dụ cụ thể:

Ví Dụ 1: Cho tam giác ABC có các cạnh a = 7 cm, b = 8 cm, và góc C = 60°. Tính cạnh c và diện tích của tam giác.

• Tính cạnh c: Sử dụng định lý Cosin:c2=a2+b2−2abcosCc2=72+82−2⋅7⋅8⋅cos60°c2=49+64−56c2=57c=57​≈7.55 cm
• Tính diện tích: Sử dụng công thức:S=21​absinCS=21​⋅7⋅8⋅sin60°S=21​⋅7⋅8⋅23​​S=143​≈24.25 cm2

Ví Dụ 2: Cho tam giác ABC có các cạnh a = 13 cm, b = 14 cm, và c = 15 cm. Tính các góc của tam giác và diện tích của tam giác.

• Tính góc A: Sử dụng định lý Cosin:cosA=2bcb2+c2−a2​cosA=2⋅14⋅15142+152−132​cosA=420196+225−169​cosA=420252​cosA=0.6A=cos−1(0.6)≈53.13°
• Tính diện tích: Sử dụng định lý Heron:p=2a+b+c​=213+14+15​=21 cmS=p(p−a)(p−b)(p−c)​S=21(21−13)(21−14)(21−15)​S=21⋅8⋅7⋅6​S=7056​≈84 cm2

8. Học Trực Tuyến Với toliha.vn

Trang web toliha.vn là một nguồn tài liệu hữu ích cho việc học tập và ôn luyện toán học trực tuyến. Tại đây, bạn có thể tìm thấy nhiều bài học, bài tập và tài liệu ôn thi giúp nâng cao kỹ năng toán học của mình. Đặc biệt, trang web cung cấp các bài học liên quan đến hệ thức lượng trong tam giác, giúp bạn hiểu rõ hơn về các khái niệm và công thức toán học.

9. Kết Luận

Hệ thức lượng trong tam giác là một trong những chủ đề quan trọng trong toán học, giúp chúng ta giải quyết các bài toán liên quan đến tam giác và có nhiều ứng dụng thực tiễn trong cuộc sống. Việc nắm vững các hệ thức này không chỉ giúp bạn trong các môn học toán mà còn mở rộng hiểu biết về các ứng dụng thực tiễn. Để hiểu rõ hơn về các khái niệm và ứng dụng của hệ thức lượng trong tam giác, bạn có thể tham khảo thêm các tài liệu học tập.