Cách Tính Khoảng Cách Giữa Hai Đường Thẳng Chi Tiết và Đầy Đủ Nhất

Kiến Thức Cơ Bản về Khoảng Cách Giữa Hai Đường Thẳng

Định Nghĩa

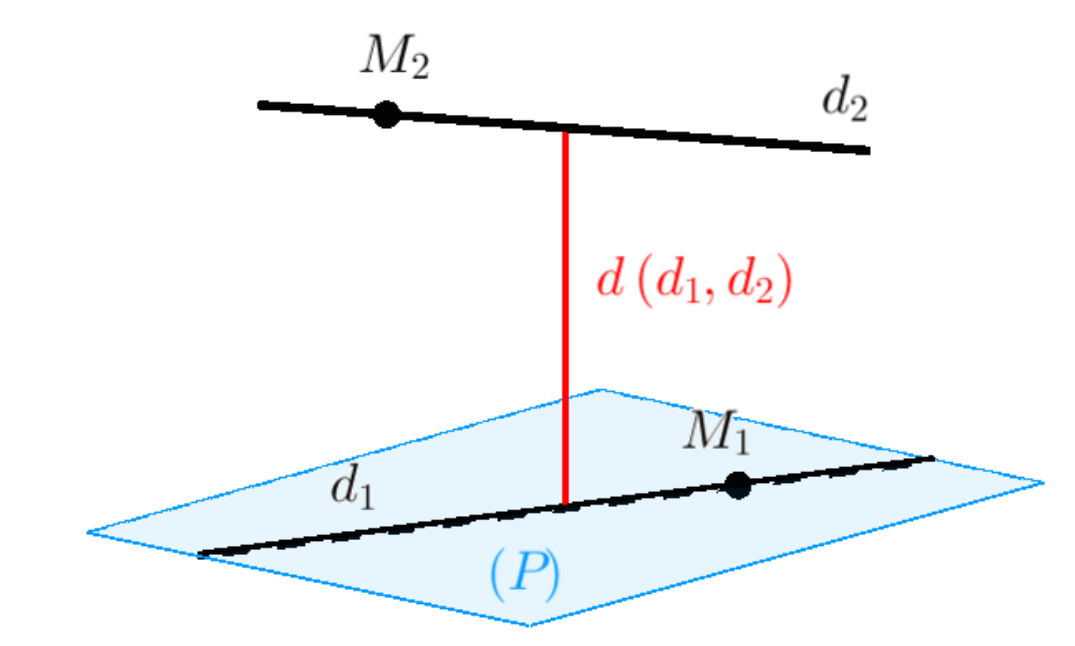
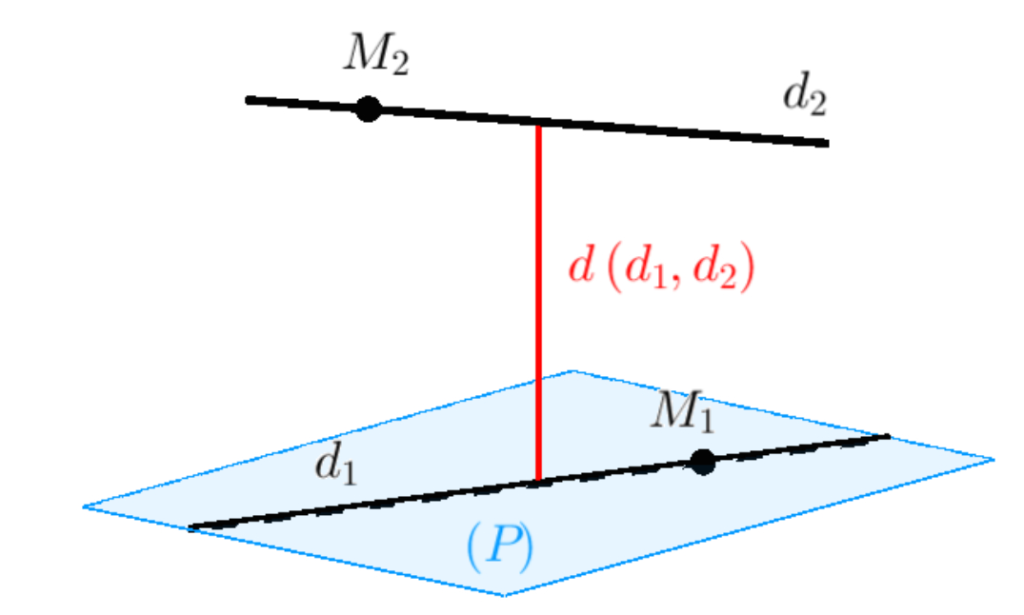
Khoảng cách giữa hai đường thẳng là độ dài đoạn thẳng ngắn nhất nối hai điểm bất kỳ thuộc hai đường thẳng đó. Trong không gian ba chiều, đoạn thẳng này luôn vuông góc với cả hai đường thẳng ban đầu.

Các Trường Hợp Đặc Biệt

1. Hai đường thẳng song song
2. Hai đường thẳng cắt nhau
3. Hai đường thẳng chéo nhau

Phương Pháp Tính Khoảng Cách Trong Mặt Phẳng

Trường Hợp Đường Thẳng Song Song

Khi hai đường thẳng song song, khoảng cách được tính theo công thức:

d = |ax₀ + by₀ + c₁ - (ax₀ + by₀ + c₂)| / √(a² + b²)

Trong đó:

• (x₀, y₀) là một điểm bất kỳ
• a, b là hệ số góc của đường thẳng
• c₁, c₂ là hệ số tự do của hai đường thẳng

Trường Hợp Đường Thẳng Cắt Nhau

Khi hai đường thẳng cắt nhau, khoảng cách giữa chúng bằng 0.

Phương Pháp Tính Trong Không Gian

Công Thức Tổng Quát

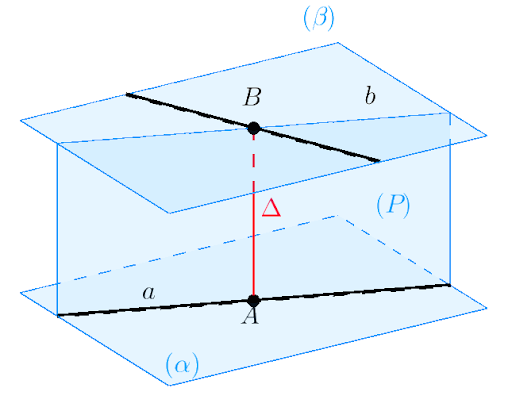
Khoảng cách giữa hai đường thẳng chéo nhau trong không gian được tính theo công thức:

d = |((a₁ × a₂) · (M₁M₂))| / |a₁ × a₂|

Trong đó:

• a₁, a₂ là vector chỉ phương của hai đường thẳng
• M₁M₂ là vector nối hai điểm bất kỳ thuộc hai đường thẳng
• × là tích có hướng
• · là tích vô hướng

Các Bước Tính Chi Tiết

1. Xác định vector chỉ phương của hai đường thẳng
2. Tính tích có hướng của hai vector chỉ phương
3. Chọn hai điểm bất kỳ thuộc hai đường thẳng
4. Áp dụng công thức tính khoảng cách

Ví Dụ Minh Họa

Ví Dụ 1: Đường Thẳng Song Song

Cho hai đường thẳng:

• d₁: 2x – 3y + 1 = 0
• d₂: 2x – 3y + 5 = 0

Giải:

d = |1 - 5| / √(2² + (-3)²)
d = 4/√13

Ví Dụ 2: Đường Thẳng Trong Không Gian

Cho hai đường thẳng:

• d₁: x = 1 + t, y = 2 + 2t, z = 3 + 3t
• d₂: x = 2 + s, y = 1 + s, z = 4 + 2s

Phương Pháp Giải Nâng Cao

Sử Dụng Vector

1. Chuyển đổi phương trình đường thẳng sang dạng vector
2. Tính các vector chỉ phương
3. Áp dụng công thức vector để tính khoảng cách

Sử Dụng Ma Trận

1. Biểu diễn các vector dưới dạng ma trận
2. Tính định thức ma trận
3. Áp dụng công thức ma trận để tìm khoảng cách

Các Bài Tập và Luyện Tập

Bài Tập Cơ Bản

1. Tính khoảng cách giữa hai đường thẳng song song
2. Xác định vị trí tương đối của hai đường thẳng
3. Tìm điểm gần nhất giữa hai đường thẳng

Bài Tập Nâng Cao

1. Bài toán về đường thẳng trong không gian
2. Bài toán kết hợp với mặt phẳng
3. Bài toán tối ưu khoảng cách

Ứng Dụng Thực Tế

Trong Kiến Trúc và Xây Dựng

1. Tính toán khoảng cách giữa các cột trụ
2. Thiết kế hệ thống dầm và thanh chống
3. Quy hoạch không gian xây dựng

Trong Công Nghệ và Kỹ Thuật

1. Thiết kế robot và máy CNC
2. Tối ưu hóa đường đi trong logistics
3. Lập trình game 3D

Kết Luận và Tổng Kết

Việc nắm vững cách tính khoảng cách giữa hai đường thẳng là kỹ năng quan trọng trong học tập và ứng dụng thực tế. Để học tập hiệu quả hơn, bạn có thể tham khảo các khóa học trực tuyến tại Toliha:

• Website: https://toliha.vn
• Hotline: 0901 86 8899
• Email: [email protected]

Tại Toliha, chúng tôi cung cấp:

1. Các khóa học online chất lượng cao
2. Giáo viên giàu kinh nghiệm
3. Tài liệu học tập đầy đủ
4. Hệ thống bài tập và kiểm tra định kỳ

Đăng ký học ngay hôm nay để nắm vững kiến thức và đạt kết quả cao trong học tập!