By TOLIHA Trong toán học, đặc biệt là trong hình học giải tích, khái niệm tâm đối xứng của đồ thị hàm số đóng vai trò quan trọng trong việc nghiên cứu tính chất đối xứng của các hàm số. Bài viết này sẽ giúp bạn hiểu rõ hơn về khái niệm này và cách xác định tâm đối xứng của đồ thị hàm số.
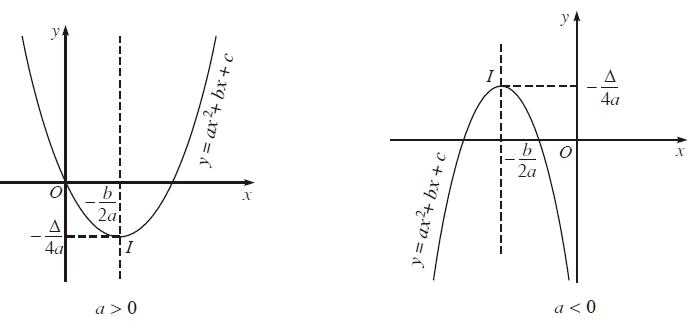
1. Khái Niệm Tâm Đối Xứng
Tâm đối xứng của đồ thị hàm số là một điểm mà khi lấy đối xứng qua điểm đó, mọi điểm trên đồ thị đều có điểm đối xứng cũng nằm trên đồ thị. Nói cách khác, nếu điểm (I(a, b)) là tâm đối xứng của đồ thị hàm số (y = f(x)), thì với mọi (x), ta có: [ f(x + a) + f(-x + a) = 2b ]
2. Tính Chất Của Tâm Đối Xứng
- Hàm số lẻ: Nếu hàm số (y = f(x)) là hàm số lẻ, thì tâm đối xứng của nó là gốc tọa độ (O(0, 0)). Điều này có nghĩa là: [ f(-x) = -f(x) ]
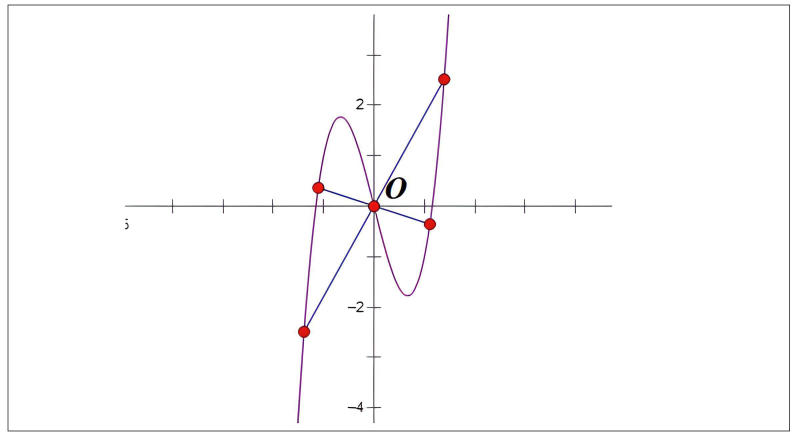
- Hàm số bậc ba: Đối với hàm số bậc ba (y = ax^3 + bx^2 + cx + d), tâm đối xứng chính là điểm uốn của đồ thị hàm số. Điểm uốn là điểm mà tại đó đồ thị chuyển từ lồi sang lõm hoặc ngược lại.
3. Phương Pháp Xác Định Tâm Đối Xứng
Để xác định tâm đối xứng của đồ thị hàm số, ta thực hiện các bước sau:
Bước 1: Giả sử (I(a, b)) là tâm đối xứng của đồ thị hàm số (y = f(x)).
Bước 2: Thực hiện phép tịnh tiến trục tọa độ (Oxy \rightarrow IXY):
[ \begin{cases} x = X + a \ y = Y + b \end{cases} ]
Bước 3: Viết công thức hàm số mới trong hệ tọa độ mới:
[ Y + b = f(X + a) ]
Bước 4: Sử dụng tính chất đối xứng để tìm (a) và (b).
4. Ví Dụ Minh Họa
Ví Dụ 1: Tìm tọa độ tâm đối xứng của đồ thị hàm số (y = x^3 + 3x^2 – 9x + 1).
Giải:
- Tính đạo hàm bậc nhất và bậc hai của hàm số: [ y’ = 3x^2 + 6x – 9 ] [ y’’ = 6x + 6 ]
- Giải phương trình (y’’ = 0): [ 6x + 6 = 0 \Rightarrow x = -1 ]
- Thay (x = -1) vào hàm số để tìm (y): [ y = (-1)^3 + 3(-1)^2 – 9(-1) + 1 = 12 ]
- Vậy tọa độ tâm đối xứng là (I(-1, 12)).
Ví Dụ 2: Tìm tọa độ tâm đối xứng của đồ thị hàm số (y = x^3 – 3x + 2).
Giải:
- Tính đạo hàm bậc nhất và bậc hai của hàm số: [ y’ = 3x^2 – 3 ] [ y’’ = 6x ]
- Giải phương trình (y’’ = 0): [ 6x = 0 \Rightarrow x = 0 ]
- Thay (x = 0) vào hàm số để tìm (y): [ y = 0^3 – 3(0) + 2 = 2 ]
- Vậy tọa độ tâm đối xứng là (I(0, 2)).
5. Ứng Dụng Của Tâm Đối Xứng
Tâm đối xứng của đồ thị hàm số không chỉ giúp chúng ta hiểu rõ hơn về tính chất đối xứng của hàm số mà còn có nhiều ứng dụng trong thực tế, như trong việc thiết kế các công trình kiến trúc, phân tích dữ liệu, và giải các bài toán tối ưu hóa.
6. Kết Luận
Việc xác định tâm đối xứng của đồ thị hàm số là một kỹ năng quan trọng trong toán học, giúp chúng ta nắm bắt được tính chất đối xứng của các hàm số và ứng dụng vào nhiều lĩnh vực khác nhau. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cơ bản và phương pháp xác định tâm đối xứng của đồ thị hàm số một cách hiệu quả.
Nếu bạn có bất kỳ thắc mắc hoặc cần thêm thông tin, hãy truy cập trang web của chúng tôi tại toliha.vn để được hỗ trợ. Chúc bạn học tốt và thành công!
Hy vọng bài viết này sẽ mang lại thông tin hữu ích và giúp bạn hiểu rõ hơn về tâm đối xứng của đồ thị hàm số. Nếu bạn có bất kỳ thắc mắc hoặc yêu cầu nào khác, đừng ngần ngại liên hệ với chúng tôi. Chúng tôi luôn sẵn sàng phục vụ bạn!
Nguyễn Thúy